Dynamical Component Analysis zur Analyse hochdimensionaler Zeitreihen. Teilprojekt 1 Hochschule Ansbach
Die Extraktion wesentlicher Inhalte aus riesigen Datenmengen ist eine der großen Herausforderungen in unterschiedlichsten wirtschaftlichen und gesellschaftlichen Bereichen. Das Projekt „Dynamical Component Analysis zur Analyse hochdimensionaler Zeitreihen“ erforscht die Analyse hochdimensionaler Zeitreihen und der Extraktion deterministischer Zusammenhänge mithilfe einer zu berechnenden Projektion in den relevanten nieder-dimensionalen Unterraum.
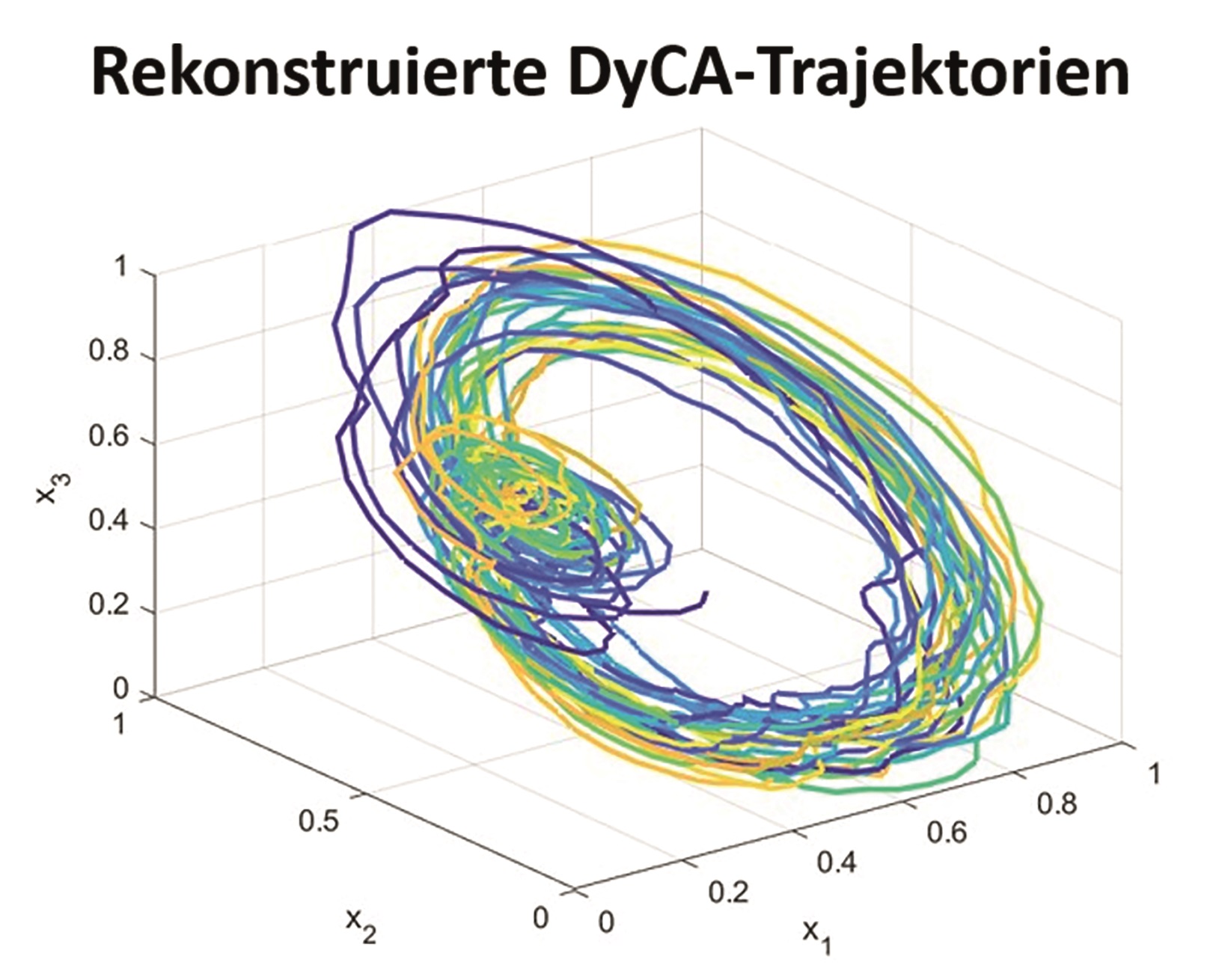
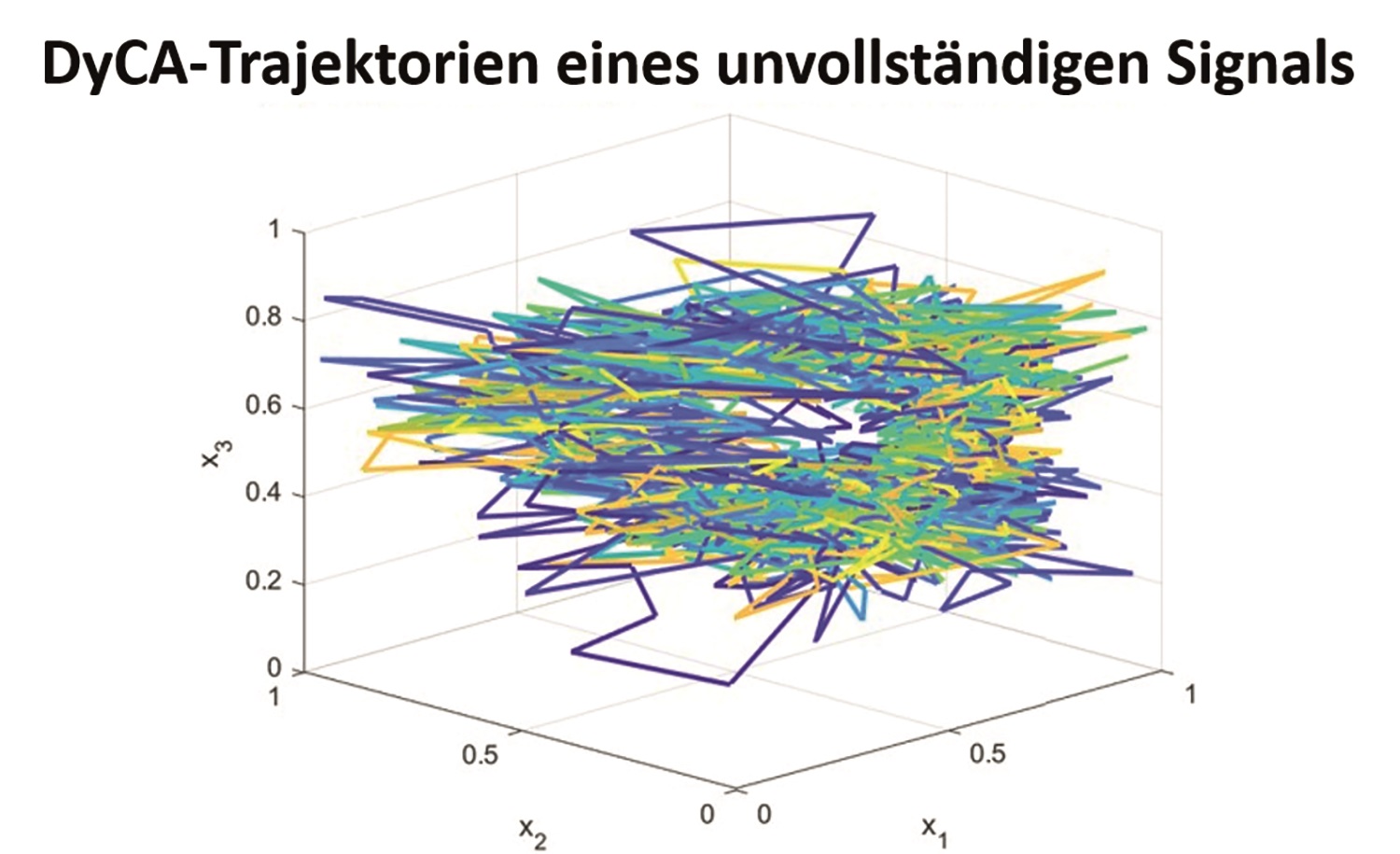
Das hierzu vor kurzem vorgeschlagene Verfahren, die Dynamical Component Analysis (DyCA), liefert die gesuchte Projektion nach Lösung eines verallgemeinerten Eigenwertproblems und der Auswahl der relevanten Eigenvektoren über Kriterien bzgl. der zugehörigen Eigenwerte.
Im Projekt erforschen die Julius-Maximilians-Universität Würzburg und die Hochschule Ansbach Grundlagen, Potenziale, Methoden und Grenzen der Anwendbarkeit des Verfahrens. DyCA kann perspektivisch in allen Anwendungsfeldern, die in Gebieten multivariater deterministischer Zeitreihen angesiedelt sind, Nutzen stiften. Mögliche Anwendungen können daher für so unterschiedliche Daten wie Wartungs- und Betriebsdaten, Wetterdaten über Strömungsdaten bis hin zu medizinischen Daten angesiedelt sein.
Im Vergleich zu etablierten Verfahren kann DyCA in geeigneten Anwendungen potenziell Zeit, Rechnerressourcen und somit Kosten sparen helfen. Zudem kann das Verfahren helfen, Daten einfacher zu visualisieren und so neue wissenschaftliche und technische Erkenntnisse ermöglichen.
Gemeinsam mit der BESA GmbH, Gräfelfing, wenden die Partner das Verfahren auf hochaufgelöste EEG-Daten für die medizinische Forschung und Diagnostik an. Eine weitere Musteranwendung ist auf dem Feld der Predictive Maintenance für Windkraftanlagen in Kooperation mit der Weidmüller Monitoring Systems GmbH.
Uhl, Christian; Stiehl, Annika; Weeger, Nicolas; Schlarb, Markus; Hüper, Knut (2024)
Frontiers in Applied Mathematics and Statistics 10-2024.
Disentangling dynamic and stochastic modes in multivariate time series
DOI: 10.3389/fams.2024.1456635
Open Access
Peer Reviewed
Hüper, Knut; Schlarb, Markus; Uhl, Christian (2024)
Automation 2024, 5(3) | 360-372.
A reformulation of the dynamical component analysis (DyCA) via an
optimization-free approach is presented. The original cost function
approach is converted into a numerical linear algebra problem, i.e., the
computation of coupled singular-value decompositions. A simple
algorithm is presented together with numerical experiments to document
the feasability of the approach. This methodology is able to recover the
mixing and state matrices of multivariate signals from high-dimensional
measured data fully.Cost Function Approach for Dynamical Component Analysis: Full Recovery of Mixing and State Matrix
DOI: 10.3390/automation5030022
Open Access
Peer Reviewed
Warmuth, Monika; Romberger, Philipp; Hüper, Knut; Uhl, Christian (2022)
Vortrag auf der International Conference on Time Series and Forecasting (ITISE) 2022, Gran Canaria, Spanien 2022.
Dynamical Component Analysis: Updated and improved algorithm, applications, and limitations
Peer Reviewed
Kern, Moritz; Korn, Katharina; Uhl, Christian (2020)
Workshop Biosignale 2020. Kiel, 11.03.2020.
Dimensionsreduktion von EEG-Daten mit Dynamical Component Analysis (DyCA)
Uhl, Christian; Kern, Moritz; Warmuth, Monika; Seifert, Bastian (2020)
IEEE Open Journal of Signal Process 1, 230-241.
Subspace Detection and Blind Source Separation of Multivariate Signals by Dynamical Component Analysis (DyCA)
Open Access
Peer Reviewed
Frühauf, Christine; Kern, Moritz; Korn, Katharina; Uhl, Christian (2020)
Ansbacher Kaleidoskop 2020. Düren: Shaker Verlag (campus_edition Hochschule Ansbach) 2020, 192-209.
Dimension reduction methods: Principle Component Analysis (PCA), Dynamical Systems Based Modeling (DSBM) and Dynamical Component Analysis (DyCA)
Open Access
Uhl, Christian (2019)
Workshop on Applied Mathematics - Dynamical Systems. IT4Innovations National Supercomputing Center. Technical University of Ostrava, 01.10.2019.
Dimension reduction methods: Principle Component Analysis (PCA), Dynamical Systems Based Modeling (DSBM) and Dynamical Component Analysis (DyCA)
Kern, Moritz (2019)
Workshop on Applied Mathematics - Dynamical Systems. IT4Innovations National Supercomputing Center. Technical University of Ostrava, 01.10.2019.
Applications of DyCA
Flammer, M (2025)
In: Aguiar, A.P., Rocha Malonek, P., Pinto, V.H., Fontes, F.A.C.C., Chertovskih, R. (eds) CONTROLO 2024. CONTROLO 2024. Lecture Notes in Electrical Engineering, vol 1325. Springer, Cham 2025.
In this paper, we show an application of spatiotemporal persistence
landscapes to real world time series. Spatiotemporal persistence
landscapes are a recent extension of persistence landscapes to time
series that capture features of the data that are persistent with
respect to time and space. We perform our analysis on EEG data to detect
absence epileptic seizures. Further, we compare two dimension reduction
techniques (DyCA and PCA) with no dimension reduction and show that the
combination of DyCA and persistent landscapes yields the best results.An Application of Spatiotemporal Persistence Landscapes and Dimension Reduction Techniques to EEG Data
DOI: 10.1007/978-3-031-81724- 3_28
Peer Reviewed
Schlarb, Markus (2025)
In: Aguiar, A.P., Rocha Malonek, P., Pinto, V.H., Fontes, F.A.C.C., Chertovskih, R. (eds) CONTROLO 2024. CONTROLO 2024. Lecture Notes in Electrical Engineering, vol 1325. Springer, Cham 2025.
The manifold of essential matrices is equipped with a one-parameter
family of (pseudo-)Riemannian metrics. For the whole family, explicit
formulas for geodesics are derived. Moreover, specific curves, so-called
quasi-geodesics, are studied and a closed form expression for a
quasi-geodesic connecting two given essential matrices is obtained.A Family of Metrics and Quasi-geodesics on the Manifold of Essential Matrices
DOI: 10.1007/978-3-031-81724-3_16
Peer Reviewed
Stiehl, Annika; Weeger, Nicolas; Uhl, Christian (2025)
In: Aguiar, A.P., Rocha Malonek, P., Pinto, V.H., Fontes, F.A.C.C., Chertovskih, R. (eds) CONTROLO 2024. CONTROLO 2024. Lecture Notes in Electrical Engineering, vol 1325. Springer 2025.
Dynamical Component Analysis (DyCA) and Dynamic Mode Decomposition (DMD), both data-driven dimension reduction methods, are introduced. After application to multivariate simulated signals the techniques of mode selection and the resulting amplitudes are compared with respect to noise robustness and sampling periods. The results indicate that DyCA is a useful alternative to DMD and outperforms DMD under certain conditions. These conditions are based on the underlying dynamics in the terms of differential equations and on the noise ratios of the signals.Comparison of Mode Selection and Reconstructions Obtained by DyCA and DMD with Respect to Noise Robustness and Sampling
DOI: 10.1007/978-3-031-81724-3_23
Peer Reviewed
Winkler, Jakob; Uhl, Christian; Geißelsöder, Stefan; Erdbrügger, Tim; Wolters, Carsten (2025)
Winkler, Jakob; Uhl, Christian; Geißelsöder, Stefan; Erdbrügger, Tim...
In: Aguiar, A.P., Rocha Malonek, P., Pinto, V.H., Fontes, F.A.C.C., Chertovskih, R. (eds) CONTROLO 2024. CONTROLO 2024. Lecture Notes in Electrical Engineering, vol 1325. Springer 2025.
This paper discusses the challenges and methods for source
reconstruction of evoked potentials using deep learning in the context
of electroencephalography (EEG). We propose the use of deep learning to
address known challenges and improve traditional approaches. We explain
the creation of a suitable dataset for solving the inverse problem,
including the simulation of neural activity and the use of lead field
matrices for the forward solution. Furthermore, we undertake a
comparative analysis of some initial deep learning models with similar
classical methods.Comparison of Classical EEG Source Analysis with Deep Learning
DOI: 10.1007/978-3-031-81724-3_24
Peer Reviewed
Uhl, Christian; Stiehl, Annika; Weeger, Nicolas (2024)
SIAM Conference on Mathematics of Data Science (MDS24) 2024.
DyCA and DMD: Differences and Similarities in Theory and Application
Peer Reviewed
Warmuth, Monika; Romberger, Philipp; Uhl, Christian; Hüper, Knut (2022)
Proceedings of the Workshop Biosignal 2022, August 24th - 26th, Dresden.
Robust Dynamical Component Analysis and its Application on Epileptic EEG and Motion Sense Data
Romberger, Philipp; Warmuth, Monika; Uhl, Christian; Hüper, Knut (2022)
Proceedings of the Workshop Biosignal 2022, August 24th - 26th, Dresden .
A Matrix Formulation of Dynamical Component Analysis (DyCA)
Romberger, Philipp; Warmuth, Monika; Uhl, Christian; Hüper, Knut (2022)
CONTROLO 2022. Lecture Notes in Electrical Engineering 930, 385-394.
Dynamical Component Analysis: Matrix Case and Differential Geometric Point of View
DOI: 10.1007/978-3-031-10047-5_34
Peer Reviewed
Kern, Moritz; Uhl, Christian; Warmuth, Monika (2021)
CONTROLO 2020. Lecture Notes in Electrical Engineering 695, 93-103.
A Comparative Study of Dynamic Mode Decomposition (DMD) and Dynamical Component Analysis (DyCA)
DOI: 10.1007/978-3-030-58653-9_9
Peer Reviewed
Korn, Katharina; Seifert, Bastian; Uhl, Christian (2019)
2019 IEEE International Conference on Acoustics, Speech and Signal Processing. Proceedings. Brighton, UK, 12.-17.05.2019. Piscataway, NJ: IEEE, 1100-1104.
Dynamical Component Analysis (DYCA) and Its Application on Epileptic EEG
DOI: 10.1109/ICASSP.2019.8682601
Open Access
Peer Reviewed
Promotionen
Generalized Dynamical Component Analysis
| Doktorand / Doktorandin | Monika Warmuth |
|---|---|
| Forschungsschwerpunkt | Smart & Green Engineering |
| Zeitraum | 15.03.2024 - 15.06.2026 |
| Wissenschaftlich betreuende Person HS Ansbach | Prof. Dr. Christian Uhl |
| Einrichtung | Hochschule Ansbach - Fakultät Technik |
| Wissenschaftlich betreuende Person (extern) |
Verbundprojektleitung
Projektdauer
01.04.2020 - 31.03.2025Projektpartner
Projektträger
Projektförderung
Förderprogramm
BMBF Mathematik für Innovationen
Adressierte SDGs (Sustainable Development Goals)
